Reinforcement learning

Reinforcement learning introduction

CS294 DRL-2017-fall(2)

Posted by thidtc on March 9, 2018

1. 马可夫链（Markov chain）

马可夫链（一阶）的定义为

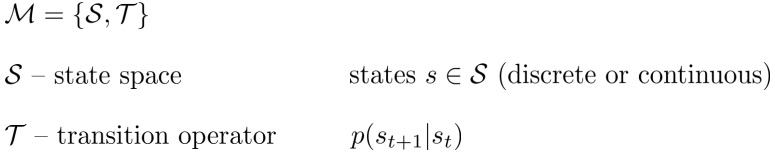
对应的概率图模型如下

马可夫链的状态仅依赖于前一个状态

2. 马可夫决策过程（Markov decision process）

MDP的定义为

对应的概率图模型为

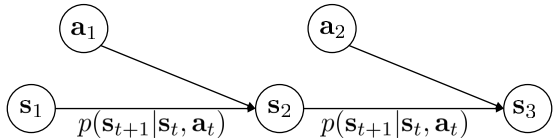
从MDP的定义可以得到以下的等式（Bellman equation）

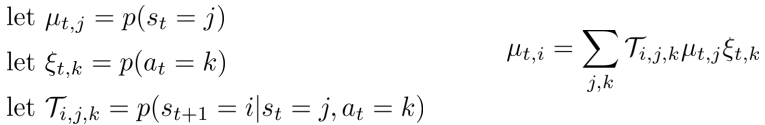
3. 部分观测马可夫决策过程（Partially observed Markov decision process）

POMDP的定义为

对应的概率图模型为

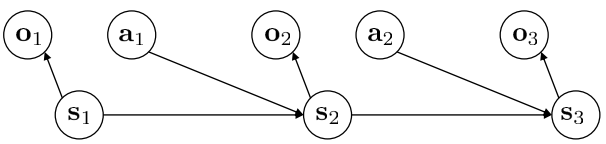
POMDP能够转化为MDP

4. 强化学习的目标

强化学习的过程如图所示

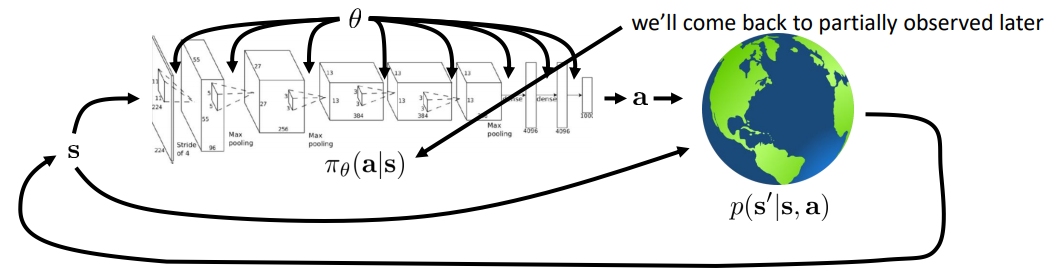
Agent通过策略 $ \pi $（policy，这里policy是通过神经网络表示）在当前状态s下选择动作a，之后，环境对agent的状态s和动作a进行相应，更新agent的状态到$ s^′ $，整个过程是一个MDP

从某个初始状态开始，可以得到agent一系列状态和动作（trajectory）的概率

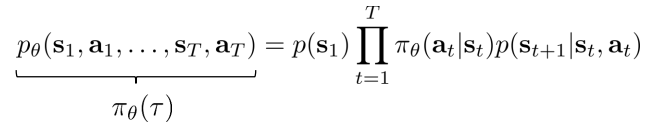
而强化学习的目标是通过优化policy，从而使得trajectory对应的reward期望最大化

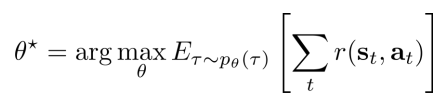
考虑agent的状态s和动作a的边缘概率（state-value margin），trajectory概率的形式可以写为

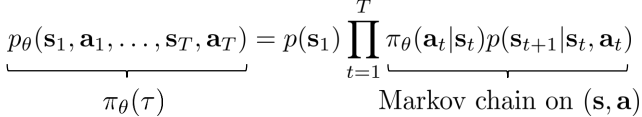
此时的概率图模型为

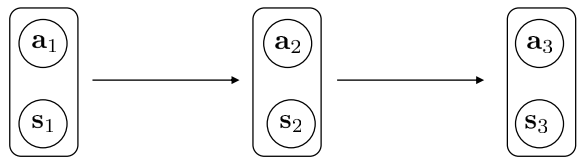
对应的转移概率为

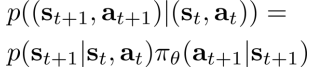
这种情况下，强化学习的目标可以改写为

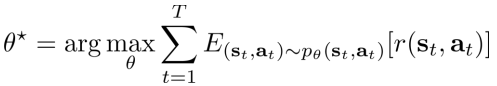
考虑无穷的MDP，即 $T -> \infty$ 的情况

考虑马可夫平稳态

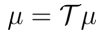
可知

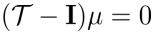
即 $\mu $ 是转移矩阵Τ特征值1对应的特征根（几乎总是存在的）

称 $\mu$ 为MDP的稳态分布（stationary distribution）

因此，在 $\mu ->\infty $ 的情况下

强化学习的目标可以改写为

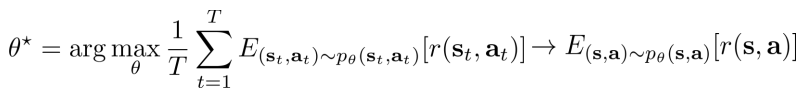
总结 强化学习的目标

  • 有限的状态转移

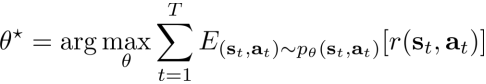
  • 无限的状态转移

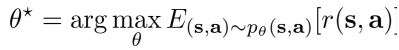
In RL，we almost always care about expectations(reward function is usually not smooth, but expectation of reward can be smooth)

(因此，强化学习的目标函数是一个期望值，因此是可导的)

5. Q-function和value function

Q-function的定义如下

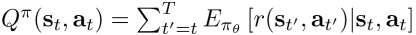
Q-function表示在 $ s_t $ 状态下采取动作 $ a_t $ 后总的reward的期望

Value function的定义如下

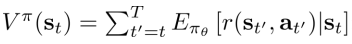
Value function表示 $ s_t $ 状态后总的reward的期望

由定义可知q-function和value function有如下的关系

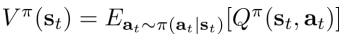
且强化学习的目标可以写成最大化

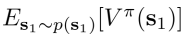
Q-function和value function在很多的RL算法中都有使用，主要使用的出发点有如下两点

  1. 如果我们有policy $ \pi $ ，并且知道该policy下的Q-function值 $ Q^\pi (s, a) $ ，则可以通过以下方式优化当前的policy $ \pi ‘ $ （Q-learning的出发点）

     当动作a满足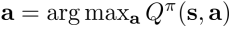

 ![](/img/reinforcement_learning_introduction/part5_figure5.png)

 设置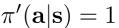

 ![](/img/reinforcement_learning_introduction/part5_figure6.png)

 易知，无论当前policy $\pi$ 如何，policy $\pi '$ 至少和 $\pi$ 一样好

  2. 计算梯度，增加一个好的动作a的概率(PG的出发点)

     易知，当动作a满足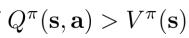

 ![](/img/reinforcement_learning_introduction/part5_figure7.png)

 则动作a比该状态下所有动作的平均水平要好，因此当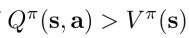

 ![](/img/reinforcement_learning_introduction/part5_figure8.png)

 可以通过修改策略policy，来增加policy选择动作a的概率

6. 强化学习算法类型

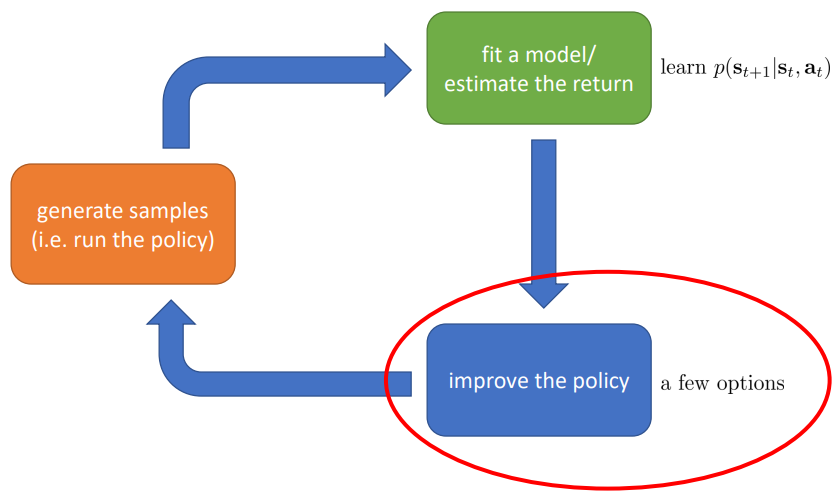
强化学习的基本步骤如下所示

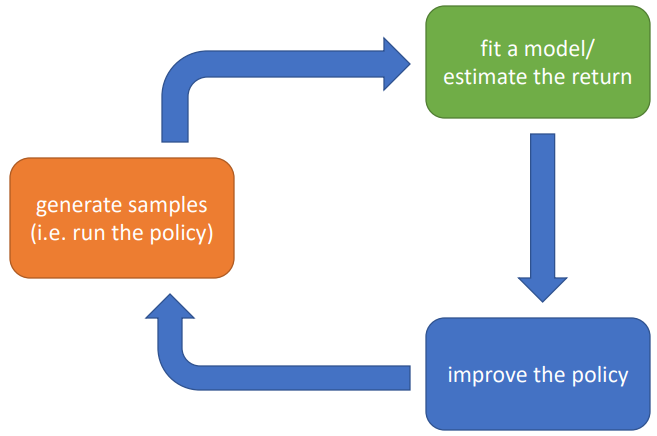
6.1 强化学习可分为以下类别

  • Policy gradient.直接对强化学习的目标函数进行优化来更新policy

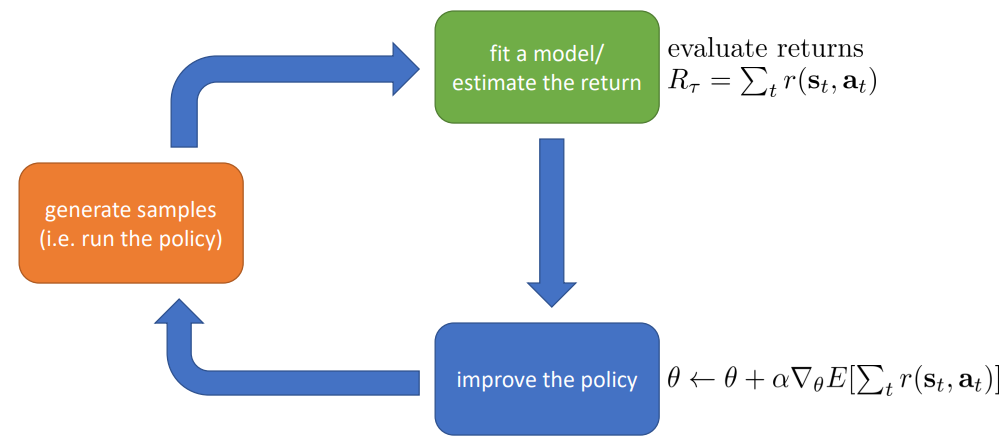
  • Value-based.估计value function和q-function的值（no explicit policy）

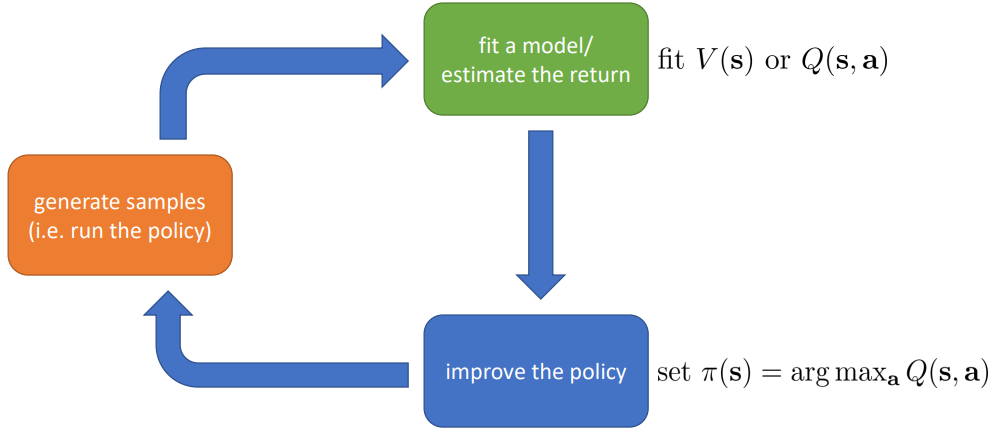
  • Actor-critic.估计value function和q-function的值，并根据这些值对policy进行更新（value function + policy gradient）

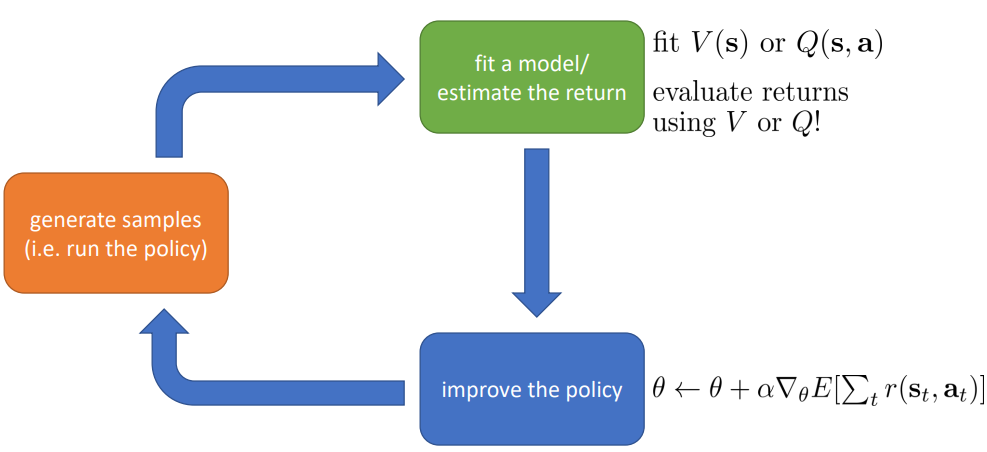
  • Model-based RL（以上均为model-free）.估计转移模型（transitino model）,并使用转移模型进行

- planning（no explicit policy）

	Trajectory optimization/optimal control 

	Discrete planning in discrete action spaces – e.g., Monte Carlo tree search

- 更新policy

	通过一定的方式将误差反向传导到policy中

	使用model学习value function

			Dynamic programming

			Dyna

6.2 不同类型算法类型下的典型算法

  • Value function fitting

    • Q-learing, DQN

    • Temporal difference learning

    • Fitted value iteration

  • Policy gradient

    • REINFORCE

    • Natural policy gradient

    • Trust region policy optimization

  • Actor-critic

    • Asynchronous advantage actor critic(A3C)

  • Model-based

    • Dyna

    • Guided policy search

7. 强化学习算法的选择

不同的情况下，会选择不同的强化学习算法

  • 不同的tradeoff

    • 采样的效率

      不同的算法有不同的采样效率

    • 算法的稳定性和易用性

      强化学习算法并不一定收敛，且收敛的结果不同，需要根据情况选择不同的算法

      • Value function fitting

        最好情况下收敛到满足最小化Bellman error（并不等价于期望reward），最坏情况下，不一定收敛

      • Model-based RL

        收敛到满足最小化Bellman error，但不能保证better model=better policy

      • Policy gradient

        优化正确的目标

  • 不同的假设

    • 强化学习的目标是确定的还是基于概率的（Stochastic or deterministic）

    • 状态和动作是连续的还是离散的（Continuous or discrete）

    • 强化学习过程是会结束的还是不会结束的（Episodic or infinite horizon）

  • 不同场景下不同算法的难度

有些场景下容易表示policy，但另一些场景下容易表示model

Catalog