1. 来源
NIPS 2017
2. 作者信息

3. 概要
本文提出了value iteration network(VIN)这个模型是一个完全可微的模型,其中包含了一个planning模块。VIN能够learn to plan,并且适用于通过使用planning预测结果的强化学习任务。VIN的关键点在于使用卷积神经网络对value-iteration算法的一个近似,因此能够使用梯度下降进行端到端的训练。本文在多个任务上进行了实验,VIN能够更好地适应新的没有遇见过的任务
4. VIN模型
假设M为当前需要求解的MDP,我们需要从中得到policy $\pi$ ,而 $\overline{M}$ 为另一个未知的MDP,但是 $\overline{M}$ 中包含和M的解 $ \pi $ 相关的信息,VIN的目标是使得 \pi $ 能够学习并且解决 $ \overline{M} $ ,同时把 $ \overline{M} $ 中的信息加入到 \pi $ 中。
假设 $ \overline{M} $ 的定义为(state, action, reward, transitions)
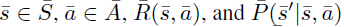
为了添加M和 $ \overline{M} $ 之间的关系,假设 $ \overline{M} $ 中的reward和transition函数都依赖于M中的观察状态 $ \phi(s) $,即
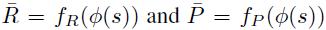
而VIN模型基于两个重要的结论
-
$ {\overline{V}}^∗ (s) $ 中包含了M ̅中所有关于optimal plan的信息,因此将$ {\overline{V}}^∗ (s) $ 作为$\pi$的输入特征能够使得$\pi$捕捉$ \overline{M} $中所有关于optimal plan的信息
-
最优policy {\overline{\pi}}^∗ (\overline{s})仅依赖于$ {\overline{V}}^∗ (s) $ 中的部分值,这是因为
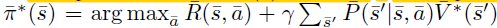
这其实非常类似于NN中的attention机制,所需要求解的值只和部分的输入有关系。 在VIN中,通过attention机制,可以获取得到attention值$\Psi(s)$,并作为$\pi$的输入
整个VIN的模型如下所示
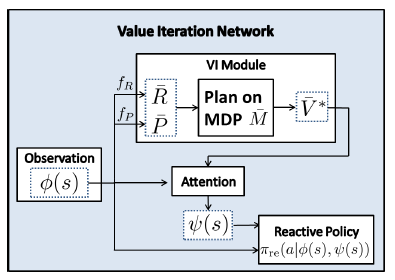
4.1 VI model
VI module的主要过程就是进行value iteration,注意到在value iteration中
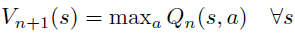
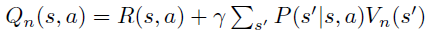
先看上面第二个公式,其中对当前状态s能够到达的其他状态s′进行遍历,然后加权求和。这个过程实际上和卷积操作很相似,只是用卷积核代替了transitions!从这个观察出发,可以通过卷积层代替上面第二个公式的操作,这样一方面使得整个过程可微,另一方面,在训练过程中,卷积核的更新过程实际上对应了对模型的建模(学习得到模型的transitions)。
再看上面的第一个公式,这是一个max操作,这个可以看作max pooling。实际上通过上诉的卷积层得到的feature map的每个channel都可以用来表示一个对应的action,因此,在channel的维度上进行max-pooling,实际上就能够表示max操作!
通过上诉的卷积层和max pooling层就能完成一次value iteration
下面整体地介绍VI Module地过程
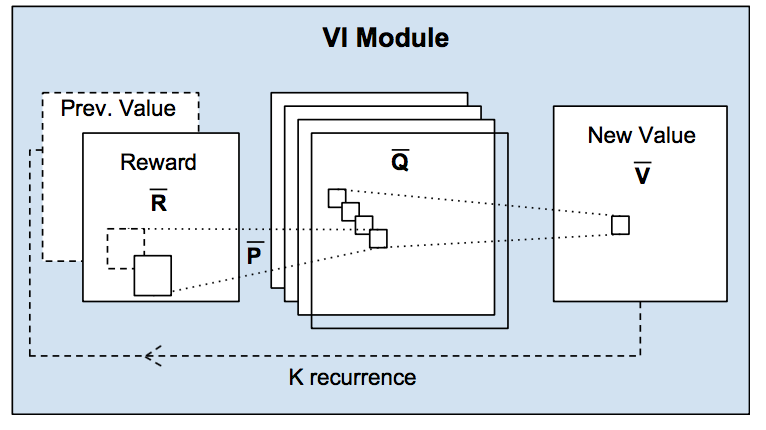
通过reward函数 $f_R$ 得到的 $ reward \overline{R} $由上诉地卷积层和max pooling层进行处理,得到迭代后地新的 $ \overline{V} $ 。然后 $ \overline{V} $ 再次和R ̅进行拼接,然后进行新一轮的value iteration。Value iteration共进行K轮
通过卷积层和max pooling层进行value iteration使得整个过程是可微的,因此使得整个过程能够端到端进行训练
5. 实验
5.1 Grid-world
测试了不同大小gridworld下从一个任务迁移到相似的任务,不同算法的效果

本文还进行了很多实验验证VIN的效果,详见原文的结果