1. 来源
NIPS 2014
2. 作者信息

3. 概要
本文提出了一个通过对抗过程对生成模型进行评估的框架,其中,同时训练了两个模型:生成模型和判别模型。这个框架对应着minimax双人博弈过程。当对生成模型和判定模型的函数进行优化时,存在唯一解,此时,生成模型能够产生和实际数据分布相同的数据分布,而判别模型的判定结果为1/2(无法判定数据为实际数据或是模型生成数据)。在实验中,该框架能够达到不错的效果
4. 模型
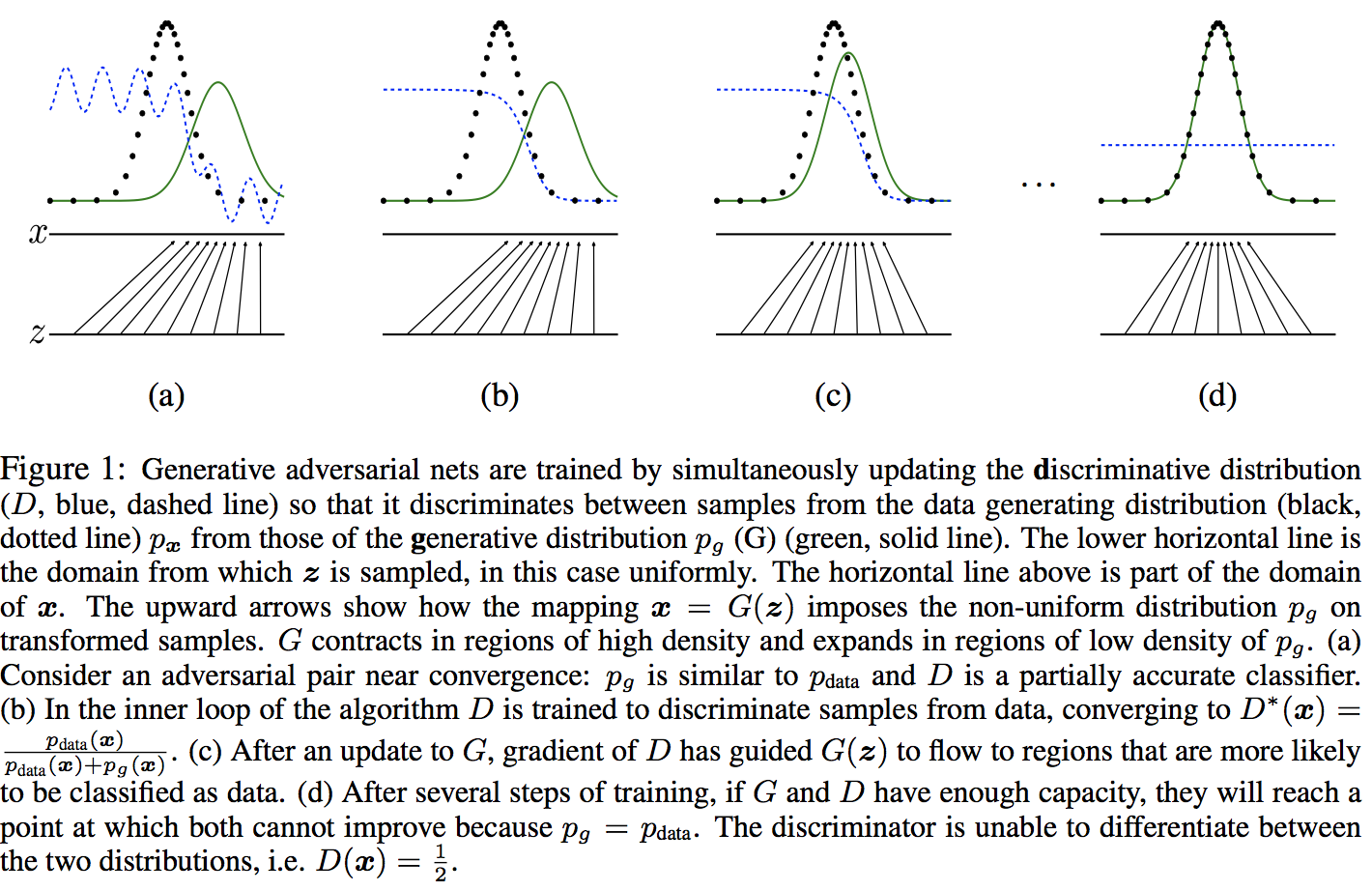
GAN的训练过程对应着生成网络G和判别网络D的双人minimax博弈过程,其价值函数为
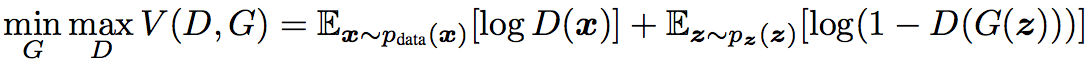
模型的训练过程中各个网络的结果如图所示
优化的方法可以通过梯度下降,轮流优化D和G,具体的算法如下

注意,实际训练过程中,在上述公式里,训练G时,通过backpropogation得到的梯度可能很小。在训练初期,当G训练不足时,D能够很好的分辨生成样本和实际样本,这种情况下log(1 −D(G(z)))⁆会饱和,因此可以通过最大化logD(G(z))⁆来替代最小化log(1 −D(G(z)))⁆。通过这种方式能够达到相同的训练结果,然而zai在训练初期能够得到更好的梯度
5. 理论分析
5.1 Global Optimality of $ p_g=p_data $
5.1.1 引论
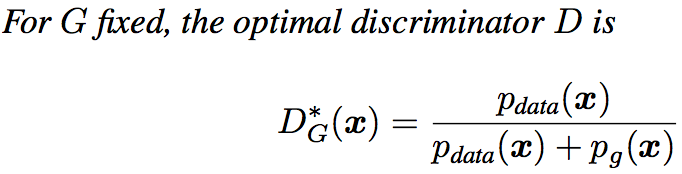
证明
当给定G时,需要最小化
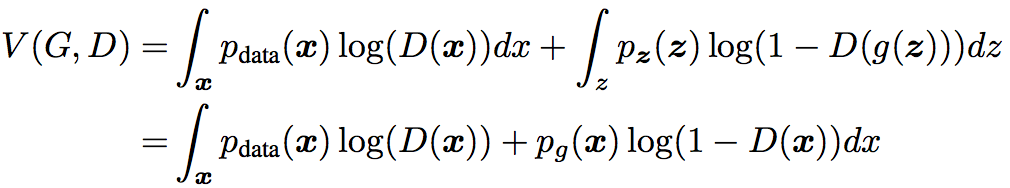
注意对于函数
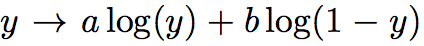
当 $ y \in [0,1⁆ $时,其最值出现在
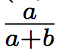
因此,得证
5.1.2 定理1
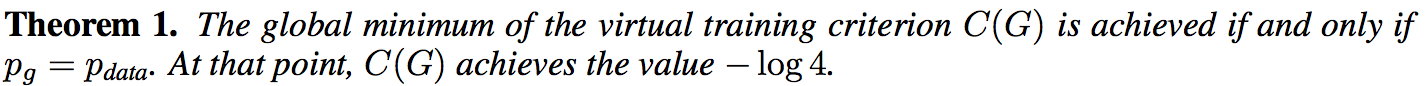
证明
把引论1的结果带入 $ V(G,D) $ ,可得
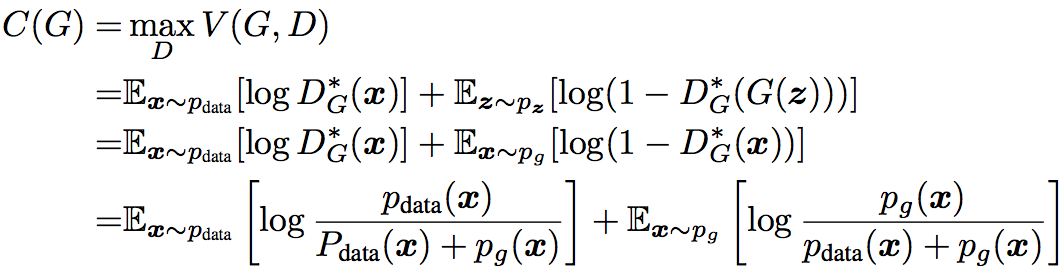
当 $ p_g=p_data $ 时,易见
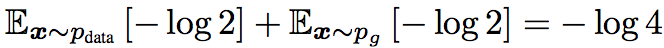
接下来证明 $ −log4 $ 是 $ C(G) $ 的下界
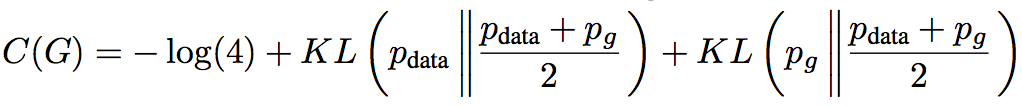
即
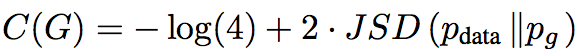
由于JS散度非负,所以 $ −log4 $ 是 $ C(G) $ 的下界
5.2 算法的收敛性
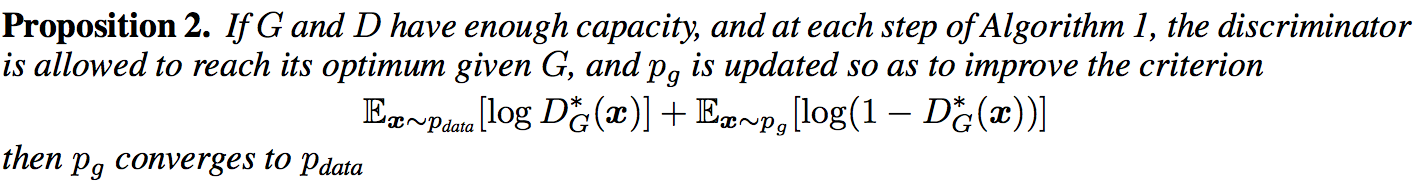
证明
结论可以直接通过一个通用性质得到
The subderivatives of a supremum of convex functions include the derivative of the function at the point where the maximum is attained
但是注意,这里,当对函数进行优化时,算法收敛,但是实际过程中,是对函数的参数优化,因此并不保证收敛,但是通常算法还是能到达不错的结果